Find Longest Path Between Two Nodes using SQL Server Recursive CTE Query
Like in a graph database, I have a set of nodes connected to each other with specific length which can be expresses as database table rows. I decided to calculate the longest path using SQL Server and SQL CTE query (Common Table Expression) returning the nodes on the longest path. The only constraints about this requirement are, the starting and ending nodes are specific. And rule is that, a node that is passed through the way can not be passed again. So on the longest path in grapg, you can not pass from a specific node or point twice.
I came across with this problem as an intelligence question in an intelligence contest at oyun.tzv.org.tr. Although it is not the correct way of solving longest path question using SQL by modelling the problem in SQL Server, I like to create solutions to such problems by programming especially in SQL.
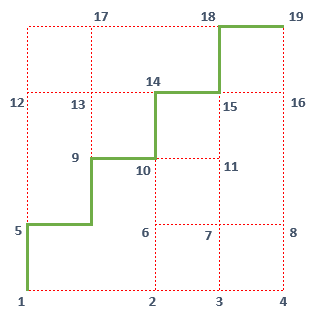
Here is "find the longest path" problem. As seen in below graph, I have a number of points aka nodes that are connected to other points via a red line. By moving along the red lines and not passing a point twice, what is the length of the longest path from bottom-left cornet to upper-right corner?
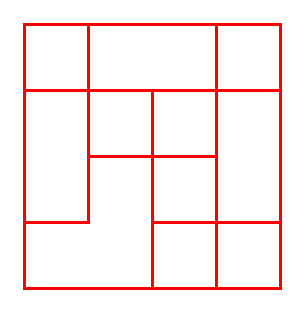
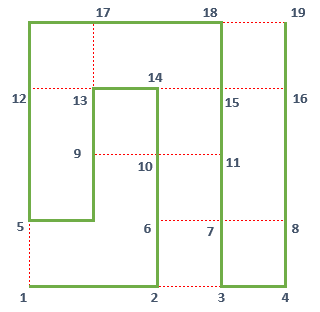
For solution, as modelling the situation I decided to give names to each intersection point using numbers.
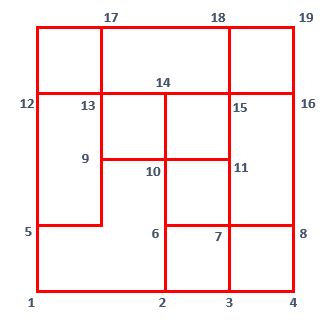
I call these intersection points nodes and started naming nodes from 1 naming lower-left corner which is the starting point.
After numbering each node, the finish node is numbered as 19 as seen in below screenshot.
To model the paths for calculating the longest path using SQL database query, I also need the length between two nodes. I added these information again on the image as follows.
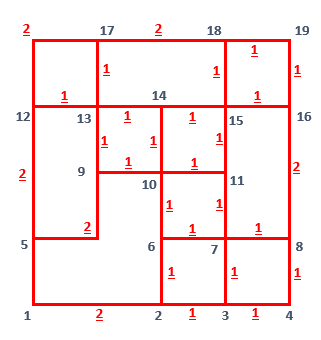
I decided to store nodes and edges length information in a SQL Server database table.
Here is the SQL database table structure and DDL Create statement.
create table Nodes (
[from] tinyint,
[to] tinyint,
[length] tinyint
)
Let's now insert graph data into Nodes table
Insert Into Nodes (
[from], [to], [length]
)
Values
(1,2,2),
(2,3,1),
(3,4,1),
(1,5,1),
(2,6,1),
(3,7,1),
(4,8,1),
(5,9,2),
(5,12,2),
(6,7,1),
(7,8,1),
(6,10,1),
(7,11,1),
(9,10,1),
(10,11,1),
(8,16,2),
(9,13,1),
(10,14,1),
(11,15,1),
(12,13,1),
(13,14,1),
(14,15,1),
(15,16,1),
(12,17,2),
(13,17,1),
(17,18,2),
(15,18,1),
(16,19,1),
(18,19,1)
And for SQL programmers please note that we have only inserted one-way from between two nodes. For example, from point 6 to 7. But the longest path might pass from node 7 and its next node in the path can be 6.
So we should INSERT the opposite directions by switching [from] and [to] into our Nodes database table.
So following is the second part of data populated into Nodes SQL table.
Insert Into Nodes (
[from], [to], [length]
)
Select
[to], [from], [length]
From Nodes
There is only two exception, since we start from node 1, it should be in the [from]. No path can pass from node 1 starting from another node.
The other exception is that, our longest path should end at node 19 which is the target node, the last node or destination of our travel.
So node 19 must be in the [to] column and cannot be in [from].
If you check above SQL Insert statement, you will see these rules are obeyed.
I find it easier to clean the problematic entries by using following DELETE command from the Nodes table.
Delete Nodes Where [from] = 19 or [to] = 1
Now for this example longest path calculation requirement, we have 54 entries in our Nodes table.
In fact it is not a necessity to remove entries like 2->1, 5->1 or 19->16 and 19->18 because we can handle these exceptions and discard them in the SQL query which we will use soon to calculate the longest path between two specific nodes (1 to 19) in the given graph relation.
Let's create out SQL query for longest path identification.
First SELECT all possible paths starting from first node 1.
Then continue by selecting second path intervals starting from these new destinations, and continue like that.
This SQL query structure will give us a SQL recursive CTE query as follows
declare @start_node int = 1
declare @end_node int = 19
;with cte as (
select
[to], [length],
convert(varchar(100), ',' + convert(varchar(2), [from]) + ',' + convert(varchar(2),[to]) + ',') as [path]
from Nodes where [from] = @start_node
union all
select
n.[to], cte.[length] + n.[length],
convert(varchar(100), cte.[path] + convert(varchar(2), n.[to]) + ',') as [path]
from cte
inner join Nodes n
on cte.[to] = n.[from] and
CHARINDEX(','+ convert(varchar(2), n.[to]) +',',cte.[path]) = 0
where n.[from] <> @end_node
)
select [length], [path]
from cte
where right([path],4) = (',' + convert(varchar(2), @end_node) + ',')
order by [length] desc
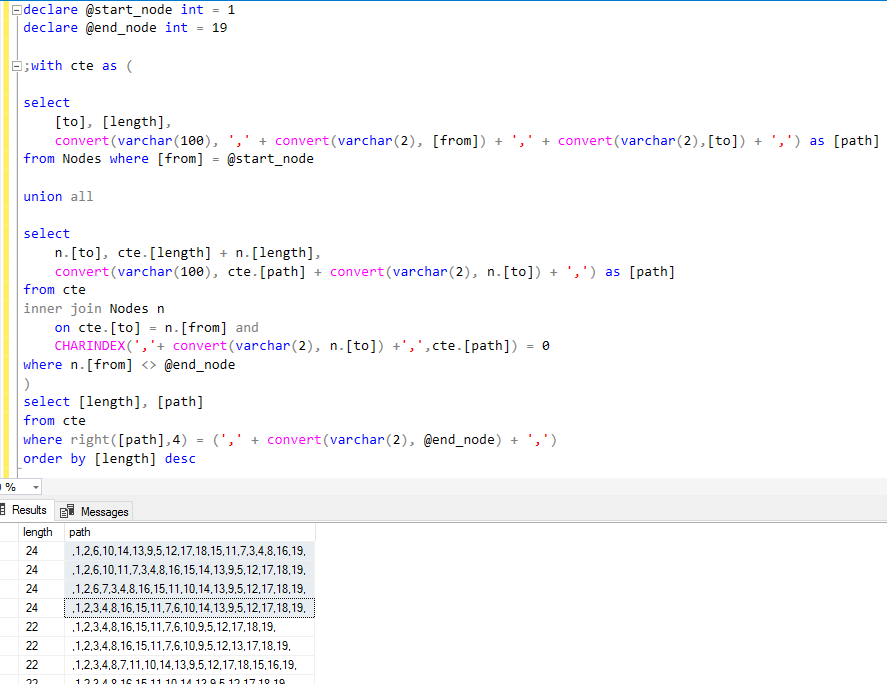
The execution of the above SQL CTE expression on Nodes database table to find the longest path from node 1 to node 19, returned 554 valid paths or valid routes.
There are 4 routes with longest path in graph with route length 24 from start node to end note:
1,2,6,10,14,13,9,5,12,17,18,15,11,7,3,4,8,16,19
1,2,6,10,11,7,3,4,8,16,15,14,13,9,5,12,17,18,19
1,2,6,7,3,4,8,16,15,11,10,14,13,9,5,12,17,18,19
1,2,3,4,8,16,15,11,7,6,10,14,13,9,5,12,17,18,19
Since I returned all valid routes starting from node 1 and ending at node 19, I also fetched the shortest paths between two.
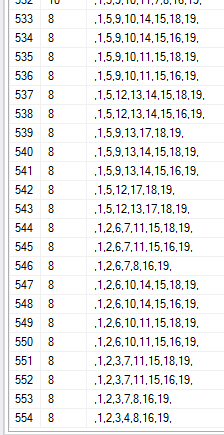
As you see there are numerous routes between two graph nodes resulting with shortest path.
The SQL Server recursive CTE query identified the shortest path length is as 8. On the other hand, the longest path between start and end nodes has a length of 24 for this sample case.
Here is one of the 4 the longest paths with total length as 24: "1,2,6,10,14,13,9,5,12,17,18,15,11,7,3,4,8,16,19"
And here is one of the shortest paths identified as having total length of 8: "1,5,9,10,14,15,18,19"
Although this approach to the solution of the longest path problem is straigt forward like a brute force attach, the cost of resources like disk space due to tempdb file extends, CPU is not linear with the number of nodes in your graph.
For example, the real problem that I tried to find the longest path in a graph which has 50 intersection points or nodes, resulted in 7270344 possible routes in total.
The execution of the above SQL Recursive CTE query last 2 hour 12 minutes on my SQL Server 2017 Developer Edition developer computer.
This is the biggest obstacle in front of the scalibility of this recursive query approach as a solution of the longest path or shortest path problem.
SQL Server database developer can encapsulate the above SQL Recursive CTE query by creating a stored procedure as seen below.
Create Procedure Find_the_Longest_Path (
@start_node tinyint,
@end_node tinyint
)
as
;with cte as (
select
[to], [length],
convert(varchar(100), ',' + convert(varchar(2), [from]) + ',' + convert(varchar(2),[to]) + ',') as [path]
from Nodes where [from] = @start_node
union all
select
n.[to], cte.[length] + n.[length],
convert(varchar(100), cte.[path] + convert(varchar(2), n.[to]) + ',') as [path]
from cte
inner join Nodes n
on cte.[to] = n.[from] and
CHARINDEX(','+ convert(varchar(2), n.[to]) +',',cte.[path]) = 0
where n.[from] <> @end_node
)
select [length], [path]
from cte
where right([path],4) = (',' + convert(varchar(2), @end_node) + ',')
order by [length] desc
GO
Using a stored procedure with starting and destination nodes as parameters and even creating a table to store outcome of the CTE and storing all desired path in this table will help T-SQL programmers to handle such long running queries.
One last note, in the beginning I used large data types for variables and calculations like Int instead of TinyInt and VarChar(max) instead of varchar(100).
Even such changes on data types you used in your SQL query can result big effects on resource consumption in a SQL problem like longest path calculation.
So if you experience resource shortage problems on your SQL Server instance machine, think about tuning your query for choosing better data types.
